Tower of Hanoi!!
Tower of hanoi is very famous and interesting game! There is a story about an ancient temple in India, it has a large room with three towers surrounded by 64 golden disks. These disks are continuously moved by priests in the temple one at a time. According to a prophecy, when the last move of the puzzle is completed the world will end!!
Game Rules:
1)Only the topmost disk can move
2)Only one disk can move at a time
3)The disk can be placed on another disk only if the other disk is larger
Your goal is to shift the stack of disk in the same order to another tower
challenge:Do it in minimum possible moves
Tower of Hanoi puzzle with n disks can be solved in minimum 2n−1 steps
while playing the game you must have noticed that you have to reconstruct the disk tower repeated that is you have to repeat similar process again and again to sovle the problem. Algorithmicly you can do this by recursion
Recursion
Recursion refers to a function calling itself.(Inception) Recursion solves such types of problems that require repetition in the process
Divide and conqure algorithm
A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly.
For instance, Imagine you have eighty coins and a set of balance scales. All the coins weigh the same, apart from one that weighs slightly less. To find this lighter coin, one solution would be to weigh and compare two coins at a time to see if there is any difference in weight – but this method would take ages. A faster way would be to divide the pile into two piles of forty and weigh these two piles against one another. You can select the lighter pile and discard the other forty coins all at once. You then repeat this process, dividing the pile into two twenties, two tens, and so on, until you narrow it down to the one coin.
one can solve the game by dividing the problem in subproblems.you can think of
first shifting n-1 disks to helper tower
then moving nth disk to destination tower and
then shifting n-1 disk to destination tower and repeating the same process.
Recursive Divide and conqure Algorithm
def towerOfHanoi(N , source, destination, auxiliary):
if N==1:
print("Move disk 1 from ",source,"to ",destination)
return
towerOfHanoi(N-1, source, auxiliary, destination)
print("Move disk",N,"from ",source,"to ",destination)
towerOfHanoi(N-1, auxiliary, destination, source)
N = 3
towerOfHanoi(N,'A','B','C')
A, C, B are the name of rods
Output
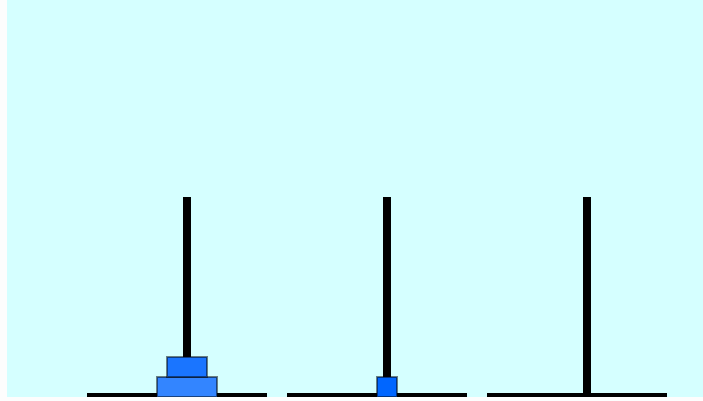
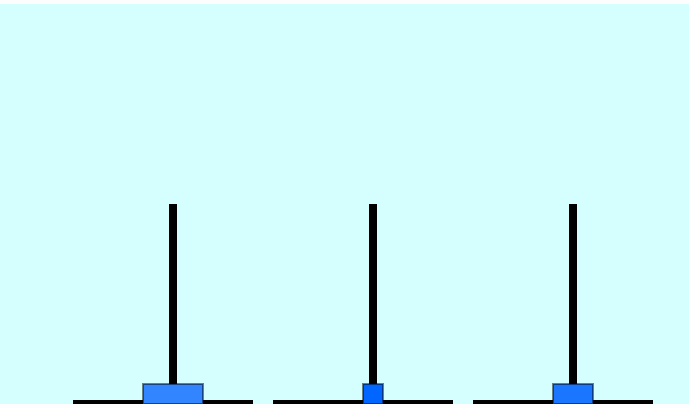
Move disk 1 from A to B Move disk 2 from A to C
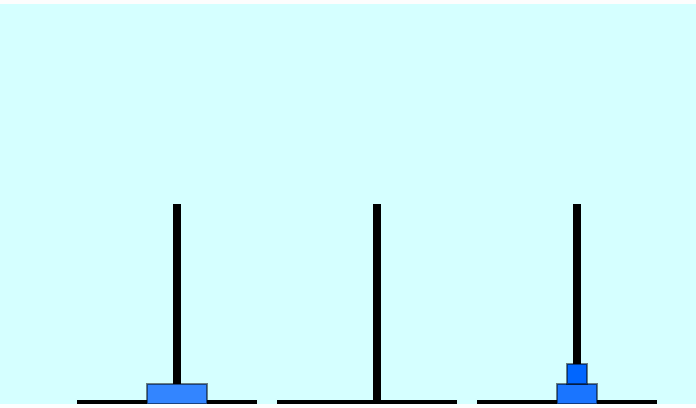
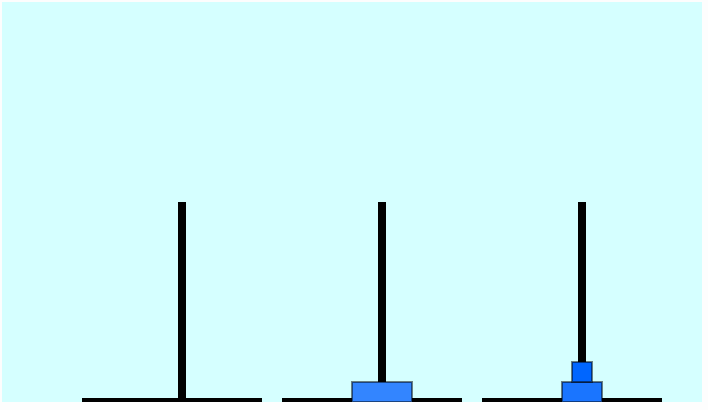
Move disk 1 from B to C Move disk 3 from A to B
Move disk 1 from C to A Move disk 2 from C to B
Move disk 1 from A to B
since we have developed an divide and conqure recursive algorithm we can find the minimum number of steps required to develop the solution.
As a result of the above procedure, the minimum number of moves hn required to solve the puzzle of n disks on three rods is given by the recurrence relation
##
hn=2hn-1+1
with h1=1.
hn =(2(2hn-2 + 1) ) + 1
= 22hn-2 + 2 + 1
= 23hn-3 + 22 + 2 + 1
=2n-1*hn-(n-1) +2n+ …… + 22 + 2 + 1
hn=2n-1,
Thus time complexity of abov Algorithm is O(2^n)
we should look for another way to count the number of moves, such as how many times each of the individual discs is moved to complete the task.The largest disc moves once, or 1 (base 2) move;
the second largest disc moves twice, or 10 (base 2) times ; the next largest disc moves four times, or 100 (base 2) times; and so on. That is, each of the terms in the sum, in the string of ones (base 2), corresponds to the number of moves made by a particular disc
To always solve the puzzle in minimum moves do this: move the smallest disk in clockwise(anticlockwise) direction. make the only possible movement. repeat.
wondering what is maximum moves to solve the puzzle?
In this case,the largest disc is moved from A to B in two (maximum) steps (A → C, C → B).
To achive above,the other (n−1) discs are shifted from A to B, then nth disc is moved A to C,
other (n−1) discs are shifted from B to A,then nth disc is moved C to B, and again, other (n−1) discs are shifted from A to B.
As a result of the above procedure, the maximum number of moves hn required to solve the puzzle of n disks on three rods is given by the recurrence relation
##
hn=3hn-1+2
with h1=2.
hn =(3(3hn-2 + 2) ) + 2
= 32hn-2 + 23 + 2
= 33hn-3 + 232 + 23 + 2
=3n-1hn-(n-1) +3n+ …… + 232 + 23 + 2
hn=3n-1,
The tower will reach all possible states
if you want to try yourself to get maximum number
1)move the smallest disk to the right,repeat this again
2)move other possible disk
3)move the smallest disk to left,repeat this again
Repeat 1,2,3
The number of possible states for a given puzzle with n disks is 3n
since each disk can be on one of the three pegs
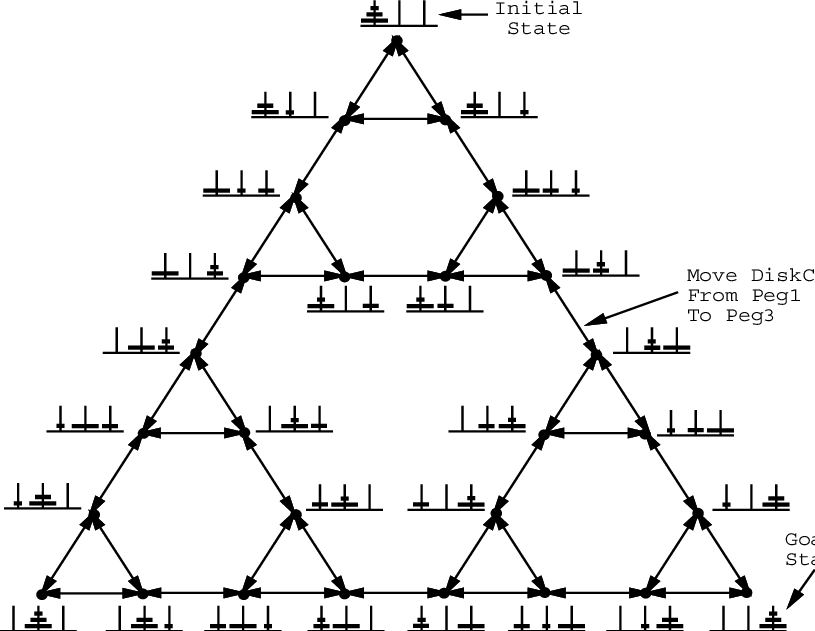
State Graph of the Three-Disk Tower of Hanoi Puzzle
The graph representing the states of momement as nodes and edges as valid move from one node to other. In the limit as n goes to infinity, this sequence of graphs can be interpreted as a discrete analogue of fractal figure the Sierpinski triangle.
Fractals
A fractal is a geometric shape that, loosely speaking, contains patterns that repeat themselves at many different scales. Fractals are often very appealing to the human eye and can be frequently found in nature – think about the branches of a tree, and how each is like a miniature tree with sub-branches of its own. Fractals are also a useful concept for solving mathematical problems
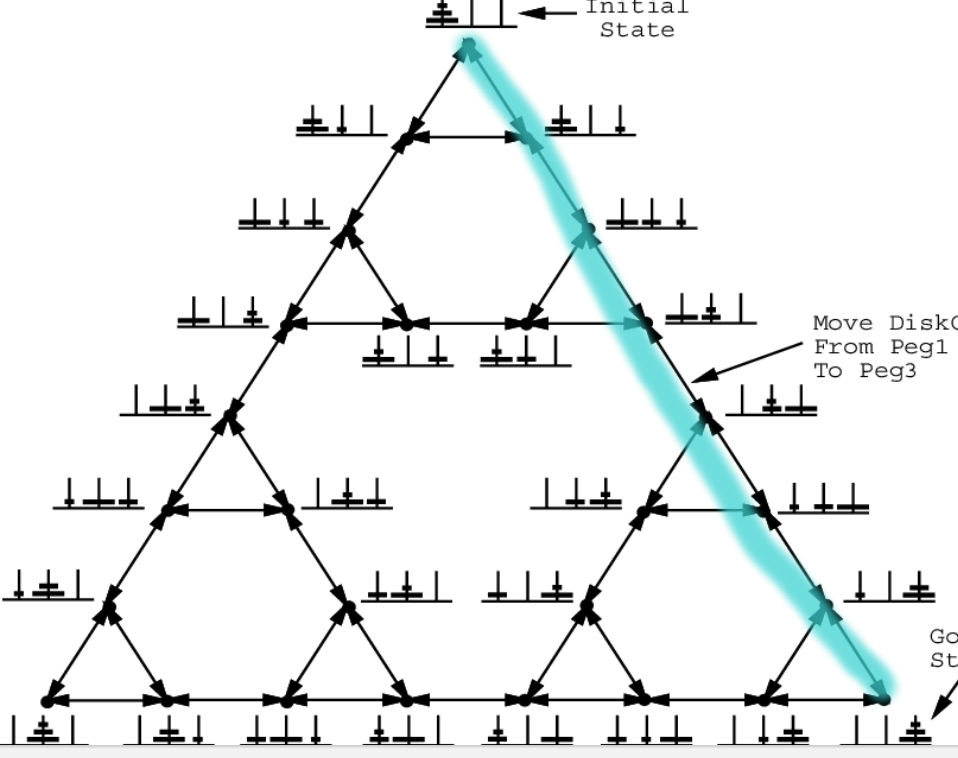
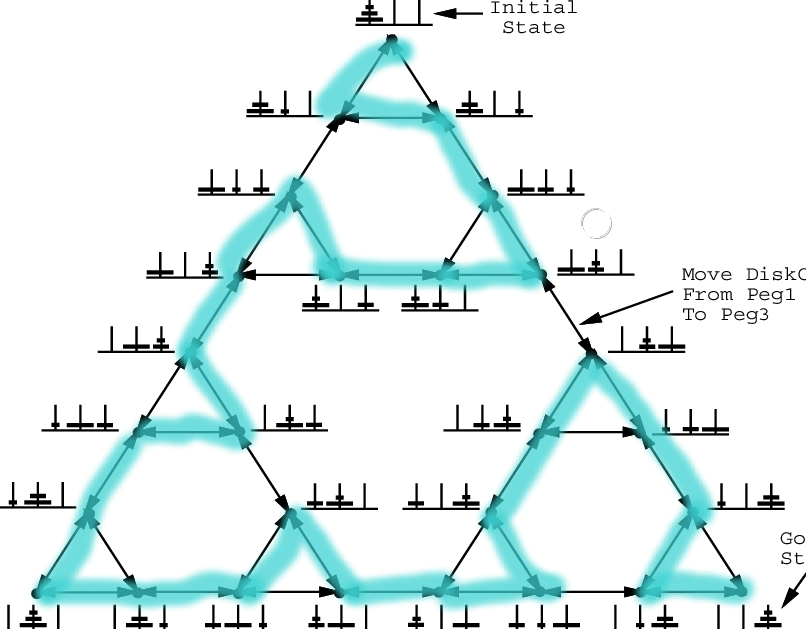
The sides of the outermost triangle represent the shortest ways of moving a tower from one peg to another one. The other diagram shows maximum moves to solve the puzzle
1) From every arbitrary distribution of disks, there is exactly one shortest way to move all disks onto one of the three pegs.
2) Between every pair of arbitrary distributions of disks there are one or two different shortest paths.
3) From every arbitrary distribution of disks, there are one or two different longest non selfcrossing paths to move all disks to one of the three pegs.
4) Between every pair of arbitrary distributions of disks there are one or two different longest non self-crossing paths.
The average length of a shortest path connecting two random states of the puzzle. While in the worst possible case the number of steps would be 2N-1 (which happens when both the initial and final states happens when both the initial and final states have all the discs concentrated on one pole, as in the original problem), Hinz’s formula says that for general initial and final states, the number of steps required would be, on average, only 466/885 times 2N, or approximately 52.6% the number of steps of the worst case. (N is the number of discs).
Connection with Binary Digits!
Disk positions can be determined from the binary representation of the move number.
The initial state being move 0, with all digits 0, and the final state being with all digits 1
The most significant bit represents the largest disk.
A value of 0 indicates that the largest disk is on the initial peg, while a 1 indicates that it’s on the final peg (right peg if number of disks is odd and middle peg otherwise).
The disk you move in step k of the solution is the disk that corresponds to the least significant 1 bit in the binary representation of k.
Example for n = 3:
step | bits | disk
1 | 001 | 1
2 | 010 | 2
3 | 011 | 1
4 | 100 | 3
5 | 101 | 1
6 | 110 | 2
7 | 111 | 1
The source and destination pegs for the mth move can also be found elegantly from the binary representation of m using bitwise operations.
Move m is from peg (m & m - 1) % 3 to peg ((m | m - 1) + 1) % 3, where the disks begin on peg 0 and finish on peg 1 or 2 according as whether the number of disks is even or odd.
Iterative Solution
import math
def towerOfHanoi(N , source, destination, auxiliary):
pegs =[ source,auxiliary, destination]
totalMoves = pow(2,N)-1
for m in range(1,totalMoves+1):
LeastSignificantSetBit =math.log2((m &-m))+1
source = pegs[(m & m - 1) % 3]
destination = pegs[((m | m - 1) + 1) % 3]
print("Move disk ",LeastSignificantSetBit," from ", source ," to ", destination)
N = 3
towerOfHanoi(N,'A','B','C')
The end of the world
when will the temple priests complete their task of moving all of the 64 disks?. The number of years to complete the task is at least: 264-1 moves ie let us suppose that priests require 1 second to perform one move. At this speed, they would require 264-1seconds to shift all discs from source tower to destination tower, which would be around 18,446,744,073,709,551,615 seconds, which would be approximately 580 billion years.(The earth is approximately 4.5 billion years old :))
Reve’s puzzle(Tower of Hanoi problem with four pegs!)
To find an optimal solution to find minimum steps to solve with n>3 pegs is not as simple as it sounds.its been Frame–Stewart algorithm The Frame–Stewart algorithm is described below: n = disks. k = pegs. T(n,k) is minimum number of moves required to transfer n disks using k pegs. The algorithm can be described recursively:
- For some l,0<=l< n, transfer the top l disks to a single peg other than the start or destination pegs, taking T(l,k) moves.
- Without disturbing the peg that now contains the top l disks, transfer the remaining n-l disks to the destination peg, using the remaining k-1 pegs, taking T(n-l,k-1) moves.
-
Transfer the top l disks to the destination peg, taking T(l,k) moves.
- The entire process takes 2T(l,k)+T(n-l,k-1) moves. Therefore, the count l should be picked for which this quantity is minimum.
for 4-pegs, T(n,4) = 2T(l,4) +T(n-l,3) = 2T(l,4)+2n-l
the optimal l equals the nearest integer to sqrt(2n).
Amazing youtube video by 3Blue1Brown
Amazing youtube video by mathologer
Towers of Hanoi – where programming techniques blend
https://en.wikipedia.org/wiki/Tower_of_Hanoi