Sudoku!

Sudoku is a very famous number game, best section of newspapers for many of us:)!Sudoku is a puzzle that has enjoyed worldwide popularity since 2005

Rules:

• Each cell on the board can have any number between 1-9.
• And we cannot have repeating numbers in the same row, column or block.
• A puzzle is solved if the cells are filled with digits 1 to 9 without violating above constraints
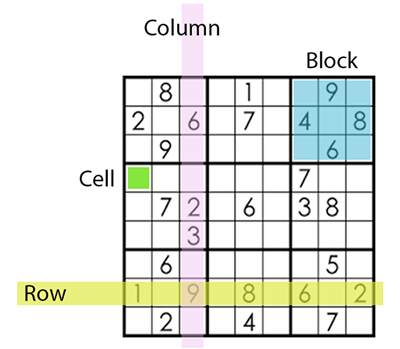
• The blue numbers in the puzzle above are clues.
• The red numbers are the ones that are placed by the player when solving the puzzle.
  you can play the puzzle by clicking on individual cells.you will get the solution of the puzzle if you pressed solution button below the puzzle.

A Sudoku puzzle’s complexity is defined by the order of the puzzle as well as the number of clues given; as the order increase and the number of clues decrease, the complexity of the puzzle increase.
As the complexity of the puzzle increase, the likelihood of finding a solution within a reasonable time decrease.
The hardest Sudoku puzzles have 17 clues, as puzzles with fewer clues will not have unique solutions.(proved in 2011(jan to dec) by Gary McGuire)
The number of possible 9 by 9 Sudoku grids is N=6670903752021072936960 which is approximately 6.671×1021

Backtracking

Sudoku can be classified as a classic search problem where you go through all the possible states in a graph to find the optimal solution. backtracking explore search tree in depth first manner and Instead of working out all the possible states - whether it leads to solution or not - backtracking builds the solution by taking step, see if it could lead to a solution, if not step backwards (backtrack) and try something else.The search tree is “pruned” by abandoning branches of the tree that would not lead to a potential solution. Thus, we’re constantly cutting down the search time and making it more efficient than an exhaustive or complete search. (Backtracking = DFS + pruning)

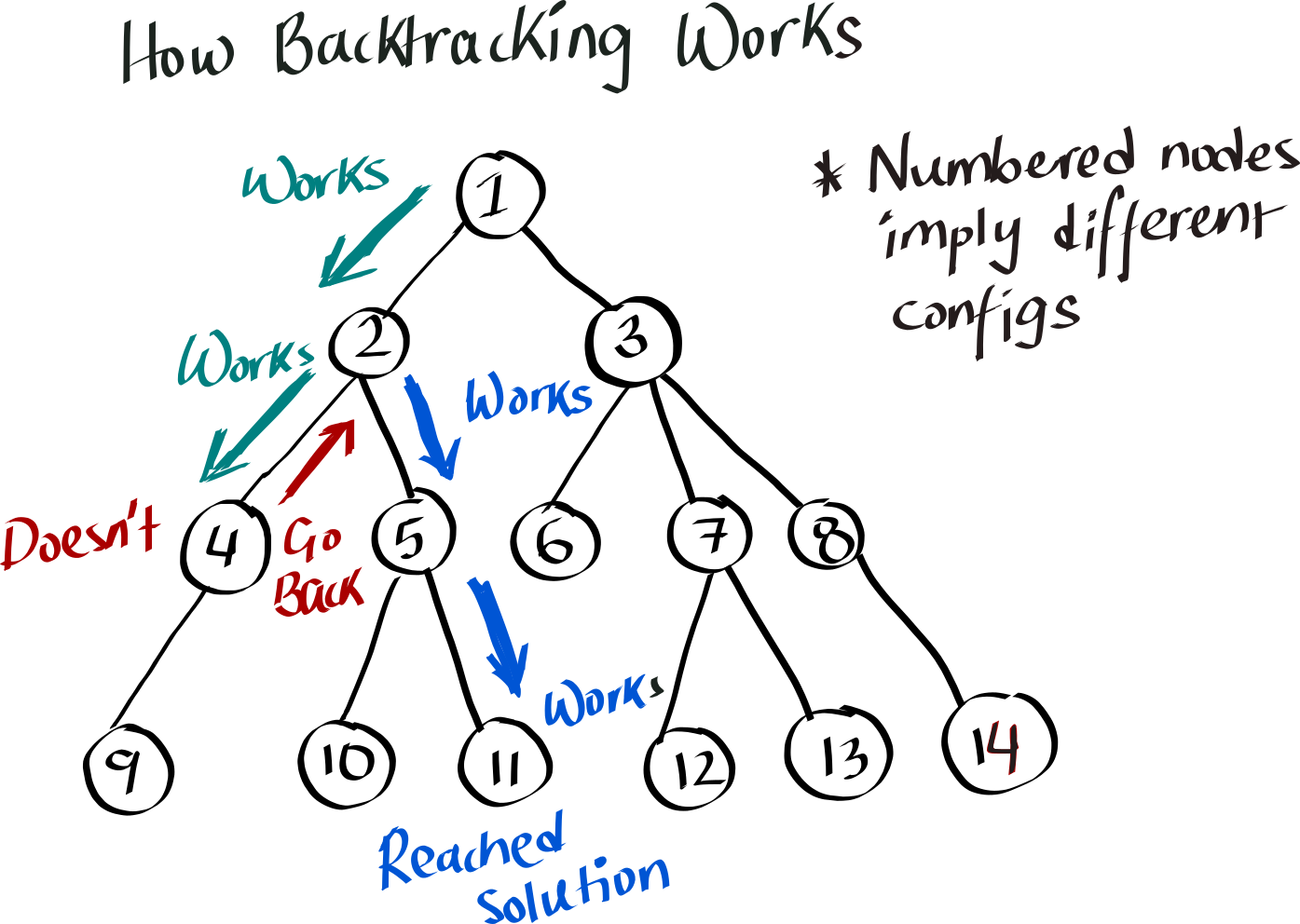
If we start filling the cells starting from 1 through 9 on the board while obeying these rules, we’ll have a bunch of different intermediate configurations of the board that may or may not reach the solution. If you work out all these possible configurations, one number at a time, it will look like a tree with multiple branches, where only one path will lead to the correct solution.
Since we need to find the path that leads to solution adnwe know the constaints, we can use Backtracking.
The algorithm will select the first empty square and try writing a “1”. If a “1” does not fit the algorithm will try a “2”, then a “3” and so forth up until “9”.
When a number is found that works in the minigrid, the column and the row of the number the algorithm will move on to the next empty square and repeat the process of trying to enter a number.
If no digit 1­-9 can exist in the current square the algorithm will backtrack to the previous one and try a new number. This process repeats until either the puzzle is solved or all possibilities have been exhausted, effectively proving that the puzzle is unsolvable.

Algorithm

function solveSudoku(sudoku) {      //sudoku is array of 81 number dipicting the puzzle    
    for (var i = 0; i < 81; i++) {
        if (sudoku[i] == 0) {               //0 represent empty cell
            for (var num of shuffle(arr)) {  //arr is [1,2,3,4,5,6,7,8,9]
                if (isSafe(i, num, sudoku)) { //isSafe() checks if placing that number violets any rule
                    sudoku[i] = num;
                    if (solveSudoku(sudoku)) {
                        return true
                    }
                    //backtrack
                    sudoku[i] = 0
                }
            }
            return false
        }
    }
}

Complexity Analysis :

• Time complexity: O(9^(n*n)).
  For every unassigned index, there are 9 possible options so the time complexity is O(9^(nn)). The time complexity remains the same but there will be some early pruning so the time taken will be much less than the naive algorithm but the upper bound time complexity remains the same.
  One programmer reported that such an algorithm may typically require as few as 15,000 cycles, or as many as 900,000 cycles to solve a Sudoku
• Space Complexity: O(n*n).

Constraint programming

In this type of programming relations between different variables are stated in the forms of rules, or constraints.
Those with experience solving Sudoku puzzles know that there are two important strategies that we can use to make progress towards filling in all the squares:
(1) If a cell has only one possible value, then eliminate that value from the cell’s peers possible value set.
(2) If a unit has only one possible place for a value, then put the value there.
The rules implemented are, as named in the paper“An Exhaustive Study of different Sudoku Solving Techniques”, Naked Single, Hidden Single, and the Lone Ranger. These rules are built on a principle of candidates for the empty cells in the puzzle. Each candidate represents a number that the cell could possibly contain in the current state of the puzzle.

• Naked Single
  If there is only one possible candidate for a blank cell (for instance when it’s the last blank cell in a row), that candidate is known as a “naked single”, and is entered into the blank cell.
• Hidden Single
  Sometimes there is only one possibility for a cell, but simply eliminating the candidates from the rows and minigrids does not make it obvious as in naked single. These kind of possible values are known as hidden singles. When a possible candidate for a cell can not be found anywhere else, that is known as a hidden single.
• Lone Ranger
  The Lone Ranger is a term for finding exclusive candidates in a row or minigrid with several empty cells with multiple candidates.For example, if a row has three empty cells with the candidates (3, 5, 7), (5, 7), (5, 7) the first cell has the “Lone Ranger”, (3), which will then be entered into the cell.

In the case that these rules are not sufficient to by themselves solve the puzzle, the backtracking algorithm will then be used for all the possible candidates. For example, if a cell can only contain the numbers 3,5,7,8, only these numbers will be tried when that cell is handled by the backtracking algorithm.

Other Backtracking Algorithm Applications

To solve crosswords, verbal arithmetic, Sudoku, and many other puzzles
combinatorial optimization.
Graph coloring problem and many more

The Math Behind Sudoku
https://www.youtube.com/watch?v=MlyTq-xVkQE&t=1s https://en.wikipedia.org/wiki/Sudoku_solving_algorithms http://www.diva-portal.org/smash/get/diva2:811020/FULLTEXT01.pdf http://norvig.com/sudoku.html