15 puzzle!!
The n2-1 puzzle is a classic reconfiguration puzzle with n2-1 uniquely labeled sliding unit squares within a n × n
board in which the goal is to slide the squares (without ever overlapping) into a target configuration.(which is asscending order of numbers )
We can slide four adjacent (left, right, above, and below) tiles into the empty space.
A 1000$ Cash prize puzzle!

Sam Loyd presented all the tiles in order, except with the 14 and the 15 swapped.
This became known as the 14-15 puzzle. Sam Loyd asked the editor of a New York newspaper to publish the puzzle in the Sunday edition.
with a reward of $1,000 for its solution.
Loyd offered a prize of AUS $1000, worth about $20,000 today, to the first person to solve his puzzle.
People all over the country tried to win this grand sum, but none succeeded.
To win the prize you had to start start with the 1 to 13 squares in order and the 14 and15 squares out of order as shown above.
What people didn’t know was that only half of all possible starting arrangements of pieces can be solved. This starting arrangements was one of the starting
positions that cannot be solved. That made it safe to advertise the $1000 prize. (Don’t worry the above puzzle is solvable:))
Why is this 15-Puzzle Impossible?
Lets connect the puzlle to mathematics first
Puzzle Maths
Initial Arrangement <—–> Initial permutation
Final Arrangement <—–> Final permutation
Allowed moves using only transposition(switching two at a time)
Fact: You can convert Any Permutation to any other permutation using only transposition.(puzzle constraint not applied)
Example:
1 2 3 4 5 to 3 4 5 2 1
1) steps :
1 2 3 4 5
5 2 3 4 1
3 2 5 4 1
3 4 5 2 1
3 transposition
Another way to reach 1 2 3 4 5 to 3 4 5 2 1
2) steps:
1 2 3 4 5
1 3 2 4 5
3 1 2 4 5
3 5 2 4 1
3 2 5 4 1
3 4 5 2 1
5 transposition
There are many other ways
but it is impossible to do it in even number of transpositions.
Fact: The numbers of steps required is not fixed but parity of that number is fixed
In the puzzle we are moving the empty tile all over the puzzle.Each move includes empty tile.
so what we need to do is , find the parity of empty tile to reach from initial position to final position.
And the parity of rearranging the whole puzzle from initial state to final as shown in example.
If this two parity is equal the puzzle is solvable.
Example:
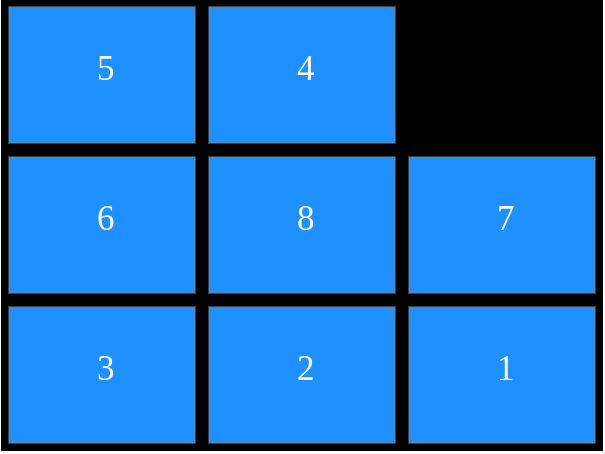
this configuration is :{5,4,0,6,8,7,3,2,1} where 0 is empty tile
1)we can move empty tile to final position by switching it with 7 and then with 1
thus parity is even
2)To rearrange the puzzle in original position
from the previous example we know that ther could be many ways but the parity will be same so we will switch it directly without the constraint of using emty tile always
5 4 0 6 8 7 3 2 1
1 4 0 6 8 7 3 2 5
1 4 5 6 8 7 3 2 0
1 4 3 6 8 7 5 2 0
1 2 3 6 8 7 5 4 0
1 2 3 4 8 7 5 6 0
1 2 3 4 5 7 8 6 0
1 2 3 4 5 7 6 8 0
1 2 3 4 5 6 7 8 0
8 transposition
which is even.thus the puzzle is solvable
In the 1000$ Cash prize puzzle only 14 and 15 was switched. The emty tile was in its place in final state.so need even parity,but the puzzle can be rearranged into final state in 1 step,thus odd parity thus non-solvable puzzle.
Algorithm to check solvability
def isSolvable(n,puzzle): //in the puzzle array emty space is denoted bu 16 ,n = lenght of puzzle
for i in range(n):
if(puzzle[i] == 16):
Emtyposition = [i/sqrt(n),i%sqrt(n)]
parityofEmty = ((sqrt(n)-1) - Emtyposition[0]+sqrt(n)-1) - Emtyposition[1])%2 //last position index - Emtyposition index
steps_to_rearrange = 0
for i in range(n):
if(puzzle[i]!=i+1):
for j in range(i+1,n):
if(puzzle[j]==i+1):
temp = puzzle[i]
puzzle[i]= i+1
puzzle[j] = temp
steps_to_rearrange++
break
if(steps_to_rearrange%2 == parityofEmty):
print("solvable")
else:
print("Not solvable")
Time Complexity: O(n^2)
Numberphile video
Another Interesting way is to check Inversions!
A pair of tiles form an inversion if the values on tiles are in reverse order of their appearance in goal state.
The idea is based on the fact the parity of inversions remains same after a set of moves, i.e., if the inversion count is odd in initial stage, then it remain odd after any sequence of moves and if the inversion count is even, then it remains even after any sequence of moves. In the goal state, there are 0 inversions. So we can reach goal state only from a state which has even inversion count.
GFG article
How can we solve the Solvable puzzle?
we will examine search techniques.
The Graph start with inital state
and its children are new states that we get by moving the emty tile.
total states of puzzle is N^2!
half of them is solvable ,so reachable states N^2!/2
thus there will be N^2/2! nodes
By brute force we can use BFS/DFS to reach the goal state.
BFS
Breadth-first search starts by searching a start node, followed by its adjacent nodes, then all nodes that can be reached by a path from the start node containing two edges, three edges, and so on. Formally, the BFS algorithm visits all vertices in a graph G that are k edges away from the source vertex ss before visiting any vertex k+1 edges away.
Algorithm
class StateNode:
def __init__(self, board,moved_tile,parent):
self.board = board
self.moved_tile = moved_tile
self.parent = parent
startpuzzle = StateNode(board,0,None)
Goal = [1,2,3,4,5,6....n]
BFS(startpuzzle,Goal):
queue = [startpuzzle]
visited = []
while (queue):
curentstate = queue.pop()
visited.append(curentstate)
moveable_tiles = moveable(curstate.moved_tile);
for ti in (moveable_tiles):
dup = currentstate.board[::]
dup[cur.moved_tile] = dup[ti]
dup[ti] = 0
repeat =0
for state in visited:
if(state == cureentstate):
repeat =1
break
if (!repeat):
stat1 = stateNode(dup,ti,currentstate)
queue.append(state1)
final.append(curentstate)
if (Goal == currentstate.board) :
break
visited.append(curstate.board)
reconstruct(final[-1])
DFS
Depth first search (DFS) algorithm starts with the initial node of the graph G, and then goes to deeper and deeper until we find the goal node or the node which has no children. The algorithm, then backtracks from the dead end towards the most recent node that is yet to be completely unexplored.
Algorithm
class StateNode:
def __init__(self, board,moved_tile,parent):
self.board = board
self.moved_tile = moved_tile
self.parent = parent
currentpuzzle = StateNode(board,0,None)
Goal = [1,2,3,4,5,6....n]
visited = []
def DFS(currentpuzzle,visited,Goal):
visited.append(curentpuzzle)
moveable_tiles = moveable(curentpuzzle.moved_tile);
for ti in (moveable_tiles):
dup = currentpuzzle.board[::]
dup[currentpuzzle.moved_tile] = dup[ti]
dup[ti] = 0
repeat =0
for state in visited:
if(state == curentpuzzle):
repeat =1
break
if (!repeat):
stat1 = stateNode(dup,ti,currentpuzzle)
DFS(stat1,visited,Goal)
if (Goal == currentpuzzle).board :
final = currentpuzzle
return
reconstruct(final)
To tranverse through each node looking for goal state will take O(Vertices+Edges) = O(N^2!/2+edges) time!
Average degree (number of neighbours) in a 3x3 search space?
- 4 corners with 2 neighbours
- 4 sides with 3 neighbours
- 1 middle with 4 neighbours
Average degree: 2 ∗4/9 + 3 ∗4/9 + 4 ∗ 1/9 = 2.67 So the number of edges in a 3x3 tile search space equals 9!/2 ∗ 2.67
time complexity = O(9!/2+9!/2*2.67) thus solving using BFS DFS would be impracticle.
A*
The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.If the bound on best possible solution itself is worse than current best (best computed so far), then we ignore the subtree rooted with the node.
Similar to branch and bound
Terminology
- Live node is a node that has been generated but whose children have not yet been generated.
- E-node is a live node whose children are currently being explored. In other words, an E-node is a node currently being expanded.
- Dead node is a generated node that is not to be expanded or explored any further. All children of a dead node have already been expanded.
Cost function(heuristic):
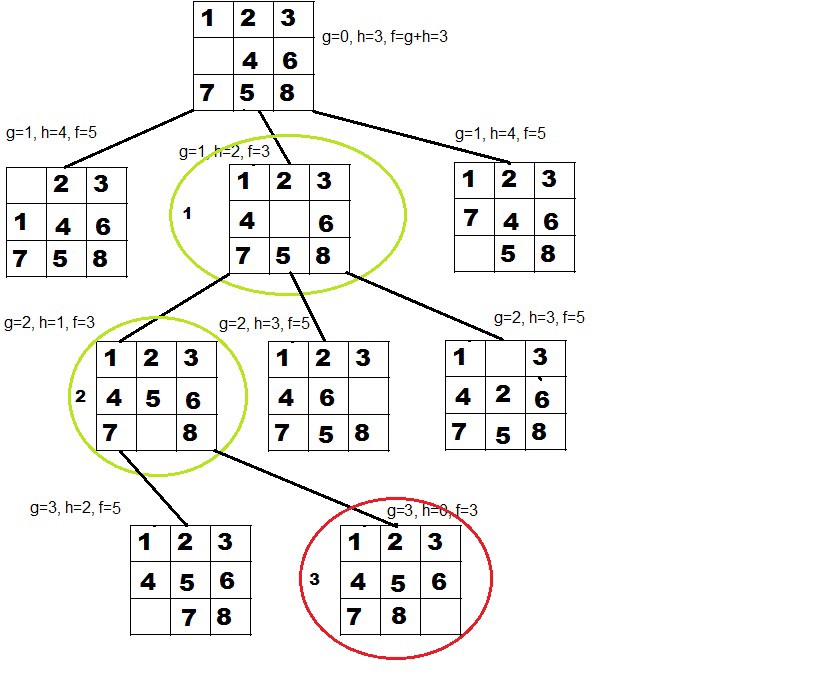
Each node X in the search tree is associated with a cost. The cost function is useful for determining the next E-node. The next E-node is the one with the least cost. The cost function is defined as
C(X) = g(X) + h(X) where
g(X) = cost of reaching the current node
from the root
h(X) = cost of reaching an answer node from X.
For the Puzzle:
c(x) = f(x) + h(x) where
f(x) is the length of the path from root to x (the number of moves so far) and
h(x) is the number of mis-placed tiles (Hamming distance) or
h(x) The sum of the minimum moves to destination (Manhatan distance:The sum of the horizontal and vertical distances between points)
using these cost function we are basically doing greedy search .It estimates how close we are to the goal.
Algorithm
class StateNode:
def __init__(self, board,moved_tile,parent, priority,moves):
self.board = board
self.moved_tile = moved_tile
self.parent = parent
self.priority = priority
self.moves = moves
startpuzzle = StateNode(board,0,None,huristic(board))
Goal = [1,2,3,4,5,6....n]
def A_star(startpuzzle,Goal):
pqueue = [startpuzzle]
visited = []
while (pqueue):
curentstate = pqueue.pop()
visited.append(curentstate)
moveable_tiles = moveable(curstate.moved_tile);
for ti in (moveable_tiles):
dup = currentstate.board[::]
dup[cur.moved_tile] = dup[ti]
dup[ti] = 0
repeat =0
for state in visited:
if(state == cureentstate.board):
repeat =1
break
if (!repeat):
stat1 = stateNode(dup,ti,currentstate,cur.moves + huristic(dup),curentstate.moves + 1)
pqueue.append(state1)
sortqueue(pqueue) //sort based on priority
if (Goal == currentstate.board) :
final = currentstate
break
visited.append(curstate.board)
reconstruct(final)
- worst-case time complexity: is exponential
- If the heuristic underestimates the cost (always less than or equal to the cost), then it finds the shortest path
- Main problem: space complexity is exponential
IDA*
It is a variant of iterative deepening depth-first search that borrows the idea to use a heuristic function to evaluate the remaining cost to get to the goal from the A* search algorithm. Since it is a depth-first search algorithm, its memory usage is lower than in A, but unlike ordinary iterative deepening search, it concentrates on exploring the most promising nodes and thus does not go to the same depth everywhere in the search tree.
IDS(Iterative Deepening Search) calls DFS for different depths starting from an initial value. In every call, DFS is restricted from going beyond given depth. So basically we do DFS in a BFS fashion.combines depth-first search’s space-efficiency and breadth-first search’s fast search (for nodes closer to root)
IDA = IDS+smart search
Goal = [1,2,3,4,5,6....n]
class StateNode:
def __init__(self, board,moved_tile,parent, priority,moves):
self.board = board
self.moved_tile = moved_tile
self.parent = parent
self.priority = priority
self.moves = moves
final = []
def IDA*():
startpuzzle = StateNode(board,0,None,huristic(board))
bound = huristic(startpuzzle)
while(1):
if(bound == sys.maxsize):
return -1
if(final==[]):
bound = search(startpuzzle,visited,bound) //bound decides to how much depth it can search
//set to min of priority of nodes that where > than bound
else:
reconstruct(final)
break
def search(currentstate,visited,bound):
visited.append(curentstate)
moveable_tiles = moveable(curentstate.moved_tile);
min = sys.maxsize
for ti in (moveable_tiles):
dup = currentstate.board[::]
dup[currnetstate.moved_tile] = dup[ti]
dup[ti] = 0
repeat =0
for state in visited:
if(state == curentstate):
repeat =1
break
f= currnetstate.moves+huristic(dup)
if (!repeat && f<=bound):
stat1 = stateNode(dup,ti,currentstate,currnetstate.moves + huristic(dup),curentstate.moves + 1)
t = search(stat1,visited,bound)
if(t<min):
min = t
else if(!repeat && f>bound && min<f):
min = f
if (Goal == currentpuzzle.board) :
final = currentstate
return min
wekipedia Parity of a permutation
http://kevingong.com/Math/SixteenPuzzle.html
https://www.ics.uci.edu/~kkask/Fall-2014%20CS271/slides/03-InformedHeuristicSearch.pdf