Domino and Tromino Tiling
puzzle:
We have an n×2 grid to be tiled.
You are given unlimited tiles of shape (2x1) and L shaped (Domino and Tromino )
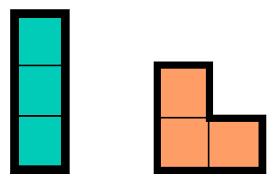
Shapes can be rotated.
The task is to find how many different options to cover the entire board in size 2xN
First let us solve easier problem ie fill the grid with only Domino.
Recursion
Recursion refers to a function calling itself.(Inception) Recursion solves such types of problems that require repetition in the process.
We will start to tile the board from the last column, i.e.; we will first tile the Nth column, then (N-1)th column, and so on.
possible cases :
- If we place the tile vertically, the problem will be converted into a sub-problem of tiling a board of size 2 * (N - 1).
- If we place the tile horizontally, 2 tiles will be required to cover the Nth and (N - 1)th column, and now the problem will be converted into a sub-problem of tiling a board of size 2 * (N - 2).
- Therefore,if count(n) is the count of ways to place tiles,count(n) can be written as below. count(n) = n if n = 1 or n = 2 count(n) = count(n-1) + count(n-2)
Recursive Agorithm
def count(n)
// Base case
if (n == 1)
return 1;
if (n == 2)
return 2;
return count(n - 1) + count(n - 2);
This pattern follows the Fibonacci Sequence
Time Complexity
The time complexity is O(2^N), where 2 * N is the size of the board.
In the worst case, it makes 2 calls for every N. Thus, the time complexity is O(2^N).
Space Complexity
The space complexity is O(N) In any case, there will be a maximum of ‘N’ function calls that will occupy O(N) space of the recursion call stack. Hence, the space complexity is given by O(N).
optimizing using Dynamic programming
Dynamic programming
Dynamic Programming is an algorithmic technique for solving a problem by recursively breaking it down into simpler subproblems and using the fact that the optimal solution to the overall problem depends upon the optimal solution to it’s individual subproblems.
DP algorithm solves each subproblem just once and then remembers its answer, thereby avoiding re-computation of the answer for similar subproblem every time.
if we take a closer look at the above explanation, we see several repetitive calculations. Thus, the problem can be considered to have a number of sub-problems, and we can store the result of these sub-problems in an array and use these results.
- Using Memoization
This approach uses recursion + memoization and breaks the problem into smaller sub-problems. The computation of subproblems is avoided if the sub-problem has already been solved before or their results are stored. - Algorithm
The output of the recursive calls can be stored in a memoization array. Before calling the recursive function, we initialize the DP array with a value equal to -1.
Before the recursive call is made, we first check whether the output is already present in the memoization array or not.
If it has already been calculated, we return the result. This helps in avoiding repetitive calculations as the value is calculated for every subtree only once.
If it’s not calculated, the result is stored in the memoization array.
memoization Agorithm
dp[1000];
fori in range(1000):
dp[i]=n
dp[0]=0
dp[1] =1
def count(n)
// If the value has been computed before, it will be returned.
if (dp[n] != -1)
return dp[n];
return dp[n] =count(n - 1) + count(n - 2);
- Bottom-Up Approach
- Algorithm
We declare a DP array of size N before calling the recursive function to store the results of the calculations.
We find a base case for the recursion and then store the result at every step in this DP array.
If the result is already present in the array, we need not calculate it again,
Else we use the DP array to calculate our answer.
Bottom-Up Approach
def count(n)
dp[n];
dp[0] = 0;
dp[1] = 1;
for i in range(2,n):
dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
Time Complexity
The time complexity is given by O(N)
Since we are using DP to store the results, every combination is computed only once.
Space Complexity
The space complexity is given by O(N) Since we are using extra space to store the results and avoid recalculation
Back to original problem.
Domino and Tromino Tiling
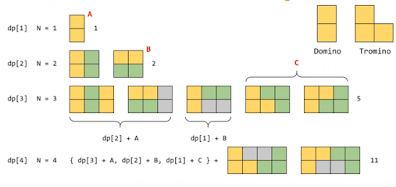
for n==1: we have only one chice - verticle Domino (A) (1-way)
for n=2: we have 2 choices
1)2 verticle Domino (1-way)
2)2 horizontal Domino(B) (1-way)
for n =3:
1) (for n=2) + A (ways for n==2 )
2) (for n=1) +B (ways for n==1)
3) placing 2 tromino such that it cover 3 tiles. (c) (2-way)
for n= 4:
1) (for n=3) + A (ways for n==3)
2) (for n=2) +B (ways for n==2)
3) 2) (for n=1) +C 2*(ways for n==2)
4) placing 2 tromino such that it cover 4 tiles..2 ways (d)
and so on
therefore
Therefore,if count(n) is the count of ways to place tiles,count(n) can be written as below.
count(n) = count(n-1) + count(n-2) + 2(count(n-3)+count(n-4)+…+count(0))
count(n-1) = count(n-2) + count(n-3) + 2(count(n-4)+…+count(0))
subtracting
count(n) = 2*count(n-1) + count(n-3)
Algorithm
count(n):
dp =[]
for i in range(n):
dp[i]=0
//base case
dp[1]=1
dp[2]=2
for i in range(3,n):
dp[i] = 2*dp[i - 1] + dp[i - 3]
return dp[N];
Time complexity: O(N)
Array iteration requires N-3 iterations where each iteration takes constant time.
Space complexity: O(N)
for maintaing Dp array
Dynamic Programming vs memoization
Memoization is the top-down technique(start solving the given problem by breaking it down)
dynamic programming is a bottom-up technique(start solving from the trivial sub-problem, up towards the given problem)
DP solves all the sub-problems, because it does it bottom-up Unlike Memoization, which solves only the needed sub-problems.
DP has the potential to transform exponential-time brute-force solutions into polynomial-time algorithms.
DP may be much more efficient because its iterative, Memoization has (often significant) overhead due to recursion.
https://www.youtube.com/watch?v=aVIFpdAg33U